
Рис. 1 - Схема замещения обратноходового преобразователя.
Рассмотрено влияние индуктивности рассеяния трансформатора на потери в снаббере для обратноходового преобразователя. Выведена формула расчета потерь через коэффициент связи трансформатора. Даны практические рекомендации по определению значения коэффициента связи по результатам измерений параметров трансформатора.
При проектировании обратноходового преобразователя, возникает необходимость защиты ключа от выброса напряжения на этапе его запирания. Как правило, эта задача решается за счет использования специальной срезающей цепи (снаббера), которая не позволяет напряжению на ключе превысить определенного, безопасного для него уровня. Простейшим вариантом, часто применяемым в преобразователях небольшой мощности, является применение для этой цели стабилитрона (Zener-диода) либо TVS (Transient Voltage Suppression) - диода. Поскольку энергия выброса при этом выделяется в снаббере, возникает необходимость количественно оценить рассеиваемую мощность, в зависимости от параметров схемы. Кроме того, при проектировании (синтезе) полезно представлять, как влияют значения, либо соотношения определенных параметров схемы, на эти потери. Ниже рассматривается вывод некоторых соотношений для обратноходового преобразователя с широтно-импульсной модуляцией второго рода (ШИМ-2), работающего в режиме прерывистого тока, позволяющих оценить эти зависимости и численно расчитать значения потерь в снаббере.
Рассмотрим схему замещения обратноходового преобразователя для установившегося режима, показанную на рис.1. Двухобмоточный трансформатор показан в виде Т-образной схемы замещения, включающей в себя
индуктивность намагничевания Lm и индуктивности рассеяния обмоток Lp1 и Lp2, приведенные к единичному витку. Vin - входное напряжение, Vo - выходное напряжение, Vz - напряжение на снаббере (стабилитроне).

Форма тока в индуктивностях Lp1 и Lp2 для случая режима прерывистого тока (РПТ) показана на рис.2.
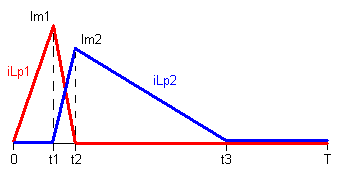
На интервале t1 < t < t2 ключ S разомкнут, D1, D2 - замкнуты. Происходит передача энергии в источники Vz и Vo. Напряжение на ключе S ограничено на уровне Vin+Vz. Ток в Lp1 спадает, в Lp2 - нарастает. Токи в диодах определяются как iD1=iLp1/w1, iD2=iLp2/w2.
К моменту t2 ток в D1 достигает нуля, и диод выключается (для простоты будем считать диоды безинерционными). Диод D2 продолжает проводить ток
на интервале t2 < t < t3, до момента t3, когда ток в нем достигнет нуля и он выключится.
Для рассмотренных интервалов справедливы соотношения (1), (2), (3), где G=t1/T, G2=(t2-t1)/T, G3=(t3-t2)/T - их относительные длительности,
Im1, Im2 - максимальные (пиковые) значения токов в Lp1 и Lp2, показанные на рис.1.
Соотношение (4) определяет равенство среднего тока в диоде D2 току нагрузки Io и позволяет получить замкнутое решение для установившегося режима.
Vd2 - падение напряжения на проводящем диоде D2 (считаем постоянной величиной). Отметим, что падением на диоде D1 мы пренебрегаем, из-за очевидной малости по сравнению с Vz.

Для случая стабилизированного преобразователя, считаем заданными параметры Vo, Vd2, Io, Vz, Vin, w1, w2, Lp1, Lp2, Lm, T. Неизвестные - G, G2, G3, Im1, Im2 могут быть найдены решением системы (1) - (4).
Интересующая нас величина - потери в стабилитроне Vz, определяется (5) - как произведение среднего тока диода D1 на напряжение Vz.

Для качественной оценки удобно воспользоваться относительной величиной Kz=Pz/Po - отношением потерь в снаббере к выходной мощности преобразователя.
После решения системы (1) - (4) и подстановки полученных значений Im1 и G2 в (5) приходим к формуле для Kz в рамках данной модели - (6).

Как правило величина рассеяния в двухобмоточном трансформаторе оценивается при помощи коэффициента связи Kc. Двухобмоточный трансформатор в общем случае описывается
системой дифференциальных уравнений (7).
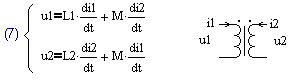
Коэффициент связи по определению это (8). А через параметры Т-образной модели трансформатора на рис.1 он может быть получет в виде (9).

Воспользовавшись этим соотношением, а также приняв что Lp1/Lm << 1, получим в конечном итоге из (6) формулу для вычисления относительных потерь в снаббере непосредственно через коэффициент связи (10).

Если индуктивность намагничивания для трансформатора может быть определена исходя из справочных данных на сердечник, то с определением индуктивностей рассеяния и коэффициента связи дело обстоит гораздо сложнее. В справочных данных можно встретить лишь оценочные величины индуктивности рассеяния на определенные типы сердечников, да и то не всегда. Поэтому заранее, на этапе синтеза, оценить индуктивность рассеяния разработчик как правило может лишь на основе эмпирических данных (опыта), если они есть.
Правда следует отметить, что в настоящее время существуют программы, позволяющие численно рассчитывать электромагнитные поля в трехмерных и двумерных моделях магнитных компонентов методом конечных элементов - Finite Element Analysys (FEA). Использование этих программ позволяет полностью рассчитать характеристики магнитных компонентов исходя из их геометрии [1].
Всё же самым достоверным методом определения параметров следует считать их экспериментальное измерение. Наиболее доступным и простым средством получения параметров трансформатора для вышеописанной модели является их измерение приборами - измерителями LRC [2]. Мы можем произвести измерения, например индуктивности первичной обмотки, при условиях разомкнутой либо замкнутой вторичной обмотки трансформатора (и наоборот), и определить затем параметры трансформатора по измеренным данным. Однако следует учитывать то обстоятельство, что указанные приборы производят измерения как правило на частоте 1кГц, которая гораздо ниже чем типичные частоты преобразователей. На низкой частоте измеряемое значение импеданса реактивной составляющей может оказаться сравнимо с активной составляющей (сопротивлением обмотки), что приведет к недопустимой погрешности. Ниже предлагается методика определения параметров трансформатора по результатам измерения LRC-метром, учитывающая сопротивления обмоток, и обеспечивающая высокую точность при определении коэффициента связи трансформатора.
Если учесть сопротивления обмоток, то двухобмоточный трансформатор будет описываться системой (11).

Рассматривая эту систему можно прийти к формуле для определения коэффициента связи через измеряемые величины (12).
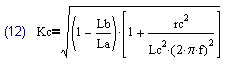
где:
La - индуктивность первичной обмотки при разомкнутой вторичной обмотке
Lb - индуктивность первичной обмотки при замкнутой вторичной обмотке
Lc - индуктивность вторичной обмотки при разомкнутой первичной обмотке
rc - сопротивление вторичной обмотки при разомкнутой первичной обмотке
f - частота измерения
Точно также можно определить взаимоиндуктивность M (13).
Поскольку количество витков в обмотках трансформатора известно (w1, w2),
теперь можно по измеренным данным также определить параметры Т-образной модели трансформатора Lm, Lp1, Lp2 - (14) - (16).

Для двух трансформаторов с одинаковыми числами витков первичной и вторичной обмоток (w1=120, w2=23), и с одним и тем же сердечником (EFD-15),
но с различным взаимным расположением обмоток (рис.3), были проведены измерения коэффициента связи и параметров Т-образной модели трансформатора по
вышеизложеной методике. Полученые значения Kc существенно различаются (0,944 для разнесенных обмоток и 0,993 для переслоенных), что подтверждает эффективность известной техники переслаивания обмоток для снижения
рассеяния в трансформаторе [3].


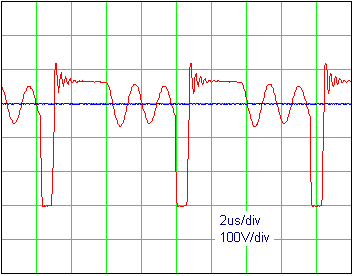
Далее были получены экспериментальные осциллограммы для схемы, показанной на рис.4, в равных условиях Vin, Vz, Vo, Io для двух вариантов трансформатора (a) и (б) (рис.5).

На рис.4 в качестве ключа и одновременно ШИМ контроллера используется микросхема TOP232G, для заведения обратной связи применена обмотка управления w3, напряжение на TVS диоде VD2 - около 120 В (Vz).
Осциллограммы на рис. 5 сняты при следующих значениях параметров: Vin=300 В, Vo=12V, Io=0.12 A. На них показаны напряжение на ключе (pin 5 DA1) - красным цветом и напряжение Vin - синим цветом. Видно, что выброс по напряжению в случае (б) существенно уже при той же амплитуде.
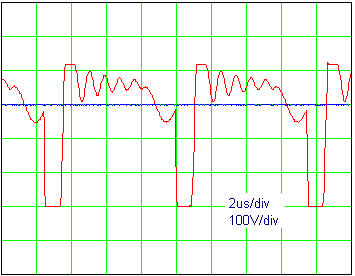 |
 |
| (a) | (б) |
Расчетные осциллограммы с Т-образной моделью трансформатора показаны на рис.6.
Исходные параметры для расчета следующие (все величины даны в СИ):
вариант (а): Vin=300 w1=120 w2=23 Vo=12 Vd2=0.7 Io=0.12 Lm=2.088e-007 Lp1=6.306e-009 Lp2=1.865e-008 T=7.6e-006 Vz=120 вариант (б): Vin=300 w1=120 w2=23 Vo=12 Vd2=0.7 Io=0.12 Lm=9.694e-008 Lp1=1.61e-010 Lp2=1.166e-009 T=7.6e-006 Vz=120Из сравнения результатов расчета и эксперимента можно заключить, что длительности рабочих интервалов схемы отражены достаточно верно при разных вариантах расположения обмоток трансформатора, и следовательно изложенный подход справедлив, несмотря на то что он не учитывает паразитные емкости ключей (отсутствие осцилляций на теоретических осциллограммах).
 |
 |
| (a) | (б) |
Но возвращаясь к цели данной статьи, следует ответить на вопрос, справедлив ли данный подход для расчета потерь в снаббере? Расчет с Т-образной моделью трансформатора по (6), дает следующие значения для рассмотренного случая: Pz(a)=0.432 Вт, Pz(б)=0.047 Вт. Расчет по формуле (10) непосредственно через коэффициент связи дает Pz(a)=0.416 Вт, Pz(б)=0.048 Вт. То есть весьма близкие к предыдущим значения.
К сожалению экспериментальное измерение потерь в снаббере в схеме на рис.4 затруднительно, поскольку достаточно точно напрямую измерить можно только напряжение Vz, но не протекающий через диод VD2
ток. Поэтому для экспериментальной проверки формулы (10) вместо Zener - снаббера, был использован RCD - снаббер, показаный на рис.7.
В этом случае потери в снаббере легко вычислить, как Pz=Vz2/Rz. Отметим, что емкость Cz достаточно велика, чтобы пренебречь пульсацией напряжения на ней.
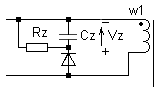
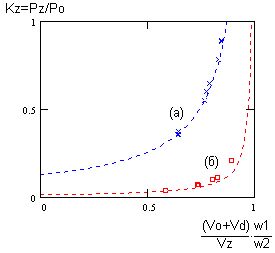
В этой схеме были проведены измерения потерь Pz при различных значениях входного напряжения и тока нагрузки. Сравнение теоретической кривой и экспериментальных точек показано на рис.8.
Здесь показаны две кривые, построеные для трансформаторов с разными значениями Kc. По оси абсцисс отложен относительный параметр - отношение выходного напряжения (с учетом падения на диоде) к приведенному напряжению снаббера.
Эта величина в явном виде присутствует в (10) и изменяется в эксперименте. Из графиков видно, что при увеличении этого параметра происходит рост потерь Pz.
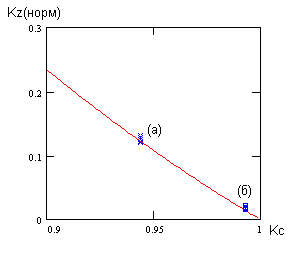
На рис.9 показана нормализованная кривая относительных потерь (17) в зависимости от коэффициента связи трансформатора Kc. Сплошной линией показана теоретическая кривая,
буквами (а) и (б) обозначены экспериментальные точки для двух вариантов трансформатора. Как видно из графика все полученые значения (при разных параметрах) попадают практически в одну точку и
хорошо согласуются с теоретической кривой.

Получена формула (10) для вычисления потерь в снаббере обратноходового преобразователя через коэффициент связи трансформатора. Исследованы и экспериментально подтверждены характеристики относительных потерь, следующие из (10). Приведена практическая методика измерения коэффициента связи трансформаторов импульсных преобразователей напряжения в случае использования стандартных измерителей LRC.