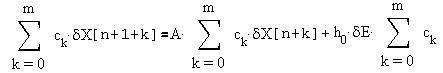
Предложен метод, позволяющий определять параметры линейного разностного уравнения, описывающего поведение на малом сигнале импульсного стабилизатора напряжения, по результатам расчета переходных процессов.

Анализ малосигнальных динамических свойств импульсных стабилизаторов напряжения (ИСН) является важной задачей при проектировании источников электропитания на их основе. Используя малосигнальную линейную модель ИСН, можно достаточно быстро и эффективно расcчитывать процессы во временной области при различных внешних воздействиях, а также строить частотные характеристики, позволяющие оценить динамические свойства системы на малом сигнале.

При использовании для анализа ИСН программ численного моделирования типа PSpice [1], как правило, отсутствуют средства, позволяющие проводить линеаризацию системы в точке установившегося режима и построение ее частотных характеристик, поскольку ИСН является дискретной системой. Для таких систем оказывается возможным только анализ во временной области. Это предоставляет возможность получить дискретные переходные характеристики в области достаточно малого сигнала.

Переходные характеристики можно также получить эксперементально. В этом случае какое либо математическое описание системы вообще отсутствует.

В настоящей статье предлагается подход, позволяющий по результатам расчета ряда переходных характеристик вычислить коэффициенты линейного разностного уравнения, описывающего поведение ИСН на малом сигнале, т.е. в конечном итоге получить аналитическое описание системы на малом сигнале, позволяющее исследовать ее динамические свойства как во временной, так и в частотной областях.

Согласно методу разностных уравнений [2,3], процессы во временной области в ИСН с широтно-импульсной модуляцией могут быть описаны рекуррентным соотношением:

X[k+1]=F(X[k],Y[k]),

(1)

где X[k] - значение вектора переменных состояния (ВПС) в начале k-го периода; Y[k] - значение вектора внешних воздействий (ВВВ) для k-го периода (считается, что ВВВ внутри периода постоянен и меняется скачком на границе следующего периода); F - некоторая нелинейная векторная функция, позволяющая определить значение ВПС в конце периода, зная его значение в начале периода. Линеаризация (1) в точке установившегося режима (X[k+1]=X[k]=Xo, Y[k]=Yo), позволяет перейти к рассмотрению разностного уравнения:

δX[k+1]=A·δX[k]+H·δY[k],

(2)

где δX[k]=X[k]-Xo, δY[k]=Y[k]-Yo - отклонения ВПС и ВВВ от своих значений в установившемся режиме, A, H - матрицы частных производных функции F по элементам, соответственно, ВПС и ВВВ в точке установившегося режима. Цель настоящей статьи - определение коэффициентов матриц A, H по результатам расчета переходных процессов.

Обозначим порядок ВПС - m, порядок ВВВ - r. Пусть на вход системы подается ступенчатое воздействие по нулевому элементу ВВВ (например это может быть напряжение питания) δY[k]₀=δE=const, δY[k]₁=δY[k]₂=.. ..=δY[k]_r-1=0, и затем рассчитывается переходный процесс. Выражение (2) в этом случае запишется в виде:

δX[k+1]=A·δX[k]+h0·δE,

(3)

где h₀ - нулевой столбец матрицы H.

Для обработки полученных в результате расчета переходного процесса данных, c целью нахождения матриц A и h₀, воспользуемся подходом, сходным с тем, который был использован в [4] для нахождения установившегося режима методом экстраполяции. Рассмотрим рекуррентное соотношение (3) на некотором участке переходного процесса, начиная с k=n, и заканчивая k=n+m:

δX[n+1]=A·δX[n]+h₀·δE

δX[n+2]=A·δX[n+1]+h₀·δE

........................

δX[n+1+m]=A·δX[n+m]+h₀·δE.

Умножим каждое из уравнений на некоторый коэффициент c_k, и затем суммируем:

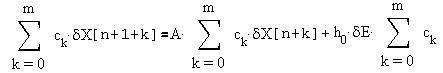(4)

Выбрав коэффициенты c_k так, чтобы

,

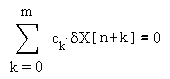(5)

получим формулу, позволяющую найти h₀:

(6)

Выполнения условия (5) можно добиться, если задаться одним из коэффициентов c_k ( например c_m ), а остальные найти из системы:

,

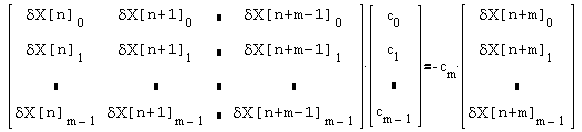(7)

где δX[n]_i - элементы вектора δX[n].

Аналогичным путем можно определить значения других столбцов матрицы H, подавая ступенчатое воздействие по другим элементам ВВВ.

Определение элементов матрицы A осуществляется следующим образом. Запишем (3) в виде:

δX[k+1]=a0·δX[k]0+a1·δX[k]1+...+am-1·δX[k]m-1+h0·δE,

(8)

где a₀.. a_m-1 - столбцы матрицы A.

Умножим, аналогично тому, как это было сделано в предыдущем случае, каждое значение формулы (8), при k=n...n+m-1, на некоторый коэффициент c_k, и суммируем полученные выражения:

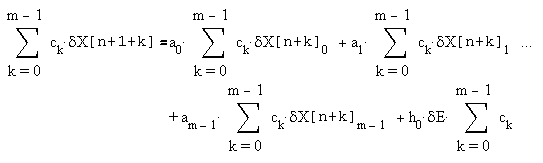(9)

Если выбрать коэффициенты таким образом, чтобы

,

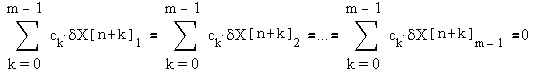(10)

то получим выражение, позволяющее найти a₀:

,

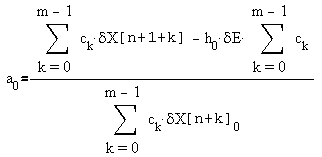(11)

Коэффициенты c_k, удовлетворяющие (10), можно получить, задавшись как и ранее, одним из них (например c_m-1), из системы:

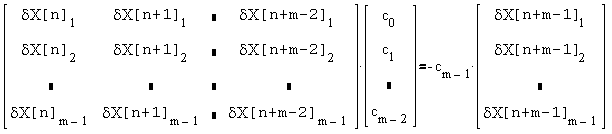(12)

Точно также можно вычислить значения остальных столбцов матрицы A.

В качестве примера рассмотрим определение коэффициентов разностного уравнения для ИСН, построенного на основе преобразователя понижающего типа, по переходным характеристикам, расчитанным с помощью программы Pspice при подаче возмущения по току нагрузки. Параметры преобразователя следующие: напряжение питания - 10 В, индуктивность дросселя - 2.5 Гн, емкость конденсатора - 12.5 Ф (дроссель и конденсатор - идеальные), сопротивление нагрузки - 5 Ом. Управление преобразователем осуществляется следующим образом: напряжение пилообразной формы Uп=a-b·t/T, где a=5.128 В, b=0.246 В, T=1 с - период коммутации, t - время прошедшее с начала периода, сравнивается с напряжением Uш=Uс+Iс·Rs, где Uс -напряжение на конденсаторе (на нагрузке), Iс - ток протекающий через конденсатор, Rs=0.111 Ом - некоторый коэффициент усиления имеющий размерность сопротивления. В качестве силовых ключей использовались встроенные модели: ключа с параметрами ron=1m и диода с параметрами n=0.1, is=1n (остальные - по умолчанию).

После подачи ступенчатого воздействия по току нагрузки путем включения дополнительного источника постоянного тока значением 0.1 А, был рассчитан фрагмент переходного процесса для переменных состояния (тока в дросселе Il и напряжения на конденсаторе Uc) в течение четырех периодов коммутации. Рассчитанные значения приведены в Таблице 1.

Таблица 1. Переходные процессы, рассчитанные с помощью PSpice.

Время, с	Il, А	Uc, В
0.000000000E+00	4.882854881E-01	4.950716496E+00
1.000000000E+00	6.074618101E-01	4.947474961E+00
2.000000000E+00	6.098288894E-01	4.949154854E+00
3.000000000E+00	5.964305997E-01	4.950350285E+00
4.000000000E+00	5.895591974E-01	4.950725555E+00

Переходные характеристики получаются при вычитании из данных Таб.1 значений переменных в установившемся режиме, существовавшем в системе до подачи возмущающего воздействия (т.е. значений переменных, стоящих в первой строке таблицы). По этим данным были определены коэффициенты матрицы A и столбца матрицы H, связанного с током нагрузки, - h₁ (считаем что нулевой элемент ВВВ - напряжения питания, первый элемент - ток нагрузки), при значении смещения n=1:

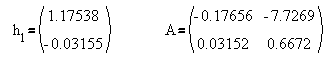
Для сравнения, приведем значения матриц A и H расчитанных при помощи метода разностных уравнений, путем аналитической линеаризации выражения (1):

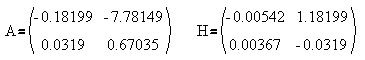
Аналогично тому, как был определен столбец h₁ , можно определить столбец h₀ , связанный с напряжением питания, путем подачи ступенчатого возмущения по этому элементу ВВВ.

Отметим, что при наличии аналитического описания ИСН на малом сигнале вида (2), могут быть построены частотные характеристики дискретной системы по формуле:

,

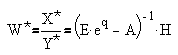(13)

(где E - единичная матрица) при подстановке q=j·ω·T и изменении ω от 0 до p/T.

Данный подход может применяться не только для анализа ИСН, но и для любых других систем, описываемых на малом сигнале разностным уравнением вида (2). При этом необходимо, чтобы ступенчатые воздействия были достаточно малы для того, чтобы реакция на них была близка к реакции линейной системы. Метод можно использовать для оценки того, насколько исследуемый переходный процесс близок к линейному. Для этого нужно последовательно вычислять матрицы A, h₀ на некотором отрезке переходного процесса, каждый раз увеличивая смещение n на единицу. Если процесс соответствует линейной системе, то вычисляемые значения матриц при разных n не должны отличаться друг от друга.

Литература.
[1] Разевиг В.Д. Применение программ P-CAD и PSpice для схемотехнического моделирования на ПЭВМ. - М.: Радио и связь,1992.
[2] Мелешин В.И. Динамические свойства преобразователей с ШИМ-2 в режимах прерывистого и непрерывного токов. - ЭТВА / Под ред. Ю.И.Конева. - М.: Радио и связь, 1986, вып. 17, с. 35-58.
[3] Соболев Л.Б. О возможности применения метода ЛЧХ к анализу преобразователей с переменной структурой. - ЭТВА / Под ред. Ю.И.Конева. - М.: Радио и связь, 1986, вып. 17, с. 88-95.
[4] Влах И., Сингхал К. Машинные методы анализа и проектирования электронных схем: Пер. с англ. - М.: Радио и связь, 1988.

© 1999, © 2008 Бердников Д.В.