 ,
,Предложен подход к сравнению частотных характеристик, получаемых при использовании методов усреднения пространства состояния и разностных уравнений, с учетом их различного физического смысла: как характеристик отражающих свойства непрерывной и дискретной систем.
В настоящее время для анализа и проектирования импульсных стабилизаторов напряжения (ИСН) с широтно-импульсной модуляцией (ШИМ) широко применяется метод усреднения пространства состояний [1,2]. Этот метод позволяет свести нелинейную дискретную систему, которой является ИСН, к некоторой непрерывной системе (в конечном итоге к линейной непрерывной системе), что позволяет использовать хорошо разработанный для непрерывных систем аппарат анализа и синтеза. Поскольку модель, полученная на основе метода усреднения (т.н. усредненная модель (УМ)), является приближенной, необходимо знать ограничения, налагаемые на ее использование при проектировании, и оценивать ее точность при анализе ИСН. Кроме того при проектировании важно уметь предсказывать как скажется на поведении системы "перевод" ее из непрерывной в дискретную форму. Поэтому еще до стадии макетирования желательно иметь некий инструмент, позволяющий получить характеристики системы с учетом пульсаций действующих в реальной схеме.
Средством, позволяющим получить точные характеристики дискретной системы, является метод разностных уравнений, применение которого для анализа ИСН описано, например, в [3,4]. Единственным допущением этого метода является условие того, что параметры схемы и внешние воздействия (источники ЭДС и тока) не меняют своих значений внутри периода коммутации, т.е. любое воздействие должно аппроксимироваться ступенчатыми функциями.
Но поскольку динамические характеристикм (переходные и час-тотные), получаемые по разностной и усредненной моделям различаются по своему физическому смыслу, необходимо учитывать это обстоятельство при их сравнении. Характеристики полученные по УМ являются характеристиками непрерывной системы и отражают поведение непрерывных величин, а характеристики полученные по разностной модели (РМ) - характеристиками дискретной системы, отражающими поведение решетчатых функций значений той или иной величины для данного периода. Кроме того, характеристики полученные по традиционной РМ обычно отражают поведение мгновенных значений переменных состояния в начале периода, тогда как поведение переменных для УМ ближе к поведению средних значений переменных в реальной системе, что следует из самого принципа построения УМ - интегрирования дифференциальных уравнений, описывающих систему, за период коммутации [2].
Цель настоящей статьи - сравнение малосигнальных частотных характеристик, полученных с помощью методов усреднения и разностных уравнений, с учетом их вышеуказанных различий.
Согласно методу разностных уравнений, поведение переменных состояния в разомкнутой системе может быть описано рекуррентным соотношением:
| X[k+1] = fp(X[k],Y[k],tи[k]), | (1) |
где X[k]- значение вектора переменных состояния (ВПС) в начале k-го периода, Y[k]-значение вектора внешних воздействий (ВВВ) для k-го периода, tи[k] - значение длительности импульса для k-го периода, fp - некоторая векторная функция, которая может быть выражена аналитически, если поведение ВПС на интервалах детерминированной структуры схемы описывается линейными дифференциальными уравнениями. В качестве элементов ВПС обычно выбирают токи в индуктивных и напряжения на емкостных элементах; ВВВ состоит из независимых источников напряжения и тока. Считается что внутри периода внешние воздействия постоянны и могут изменять свои значения скачком при переходе к следующему.
В замкнутой системе значение длительности импульса может быть в общем случае представлено в виде функции от значений ВПС в начале периода, и ВВВ для данного периода :
| tи[k]=fи(X[k],Y[k]) | (2) |
Функция fи обычно задается в неявном виде и является решением уравнения замыкания ( как правило трансцендентного) относительно переменной tи. Исключение составляет ШИМ-1, для которой функция fи может быть задана явно.
Подставляя (2) в (1), получим рекуррентное соотношение для замкнутой системы :
| X[k+1]=fз(X[k],Y[k]), | (3) |
где fз(X,Y)=fр(X,Y,fи(X,Y)).
Линеаризация (1)-(3) в точке установившегося режима (X[k+1]=X[k]=Xo, Y[k]=Yo) позволяет получить описание системы в области малого сигнала. Cоответственно для (1)-(3) в приращениях запишем:
| δX[k+1]=Ap·δX[k] + hp·δY[k] + c·δtи[k], | (4) |
| δtи[k] =b·δX[k] + v·δY[k], | (5) |
| δX[k+1]=Aз·δX[k] + hз·δY[k], | (6) |
причем Aз=Ap+c·b, hз=hp+c·v. Все коэффициенты, фигурирующие в (4)-(6) являются матрицами значений частных производных нелинейных функций fр, fи, fз по соответствующим аргументам в точке установившегося режима (Xo,Yo,tиo). Они могут быть выражены аналитически через параметры системы и значения ВПС, ВВВ и длительности импульса в установившемся режиме.
Дискретное преобразование Лапласа разностного уравнения (6) позволяет получить малосигнальные коэффициенты передачи для ВПС по элементам ВВВ в замкнутой системе:
 , , | (7) |
где E - единичная диагональная матрица. Выражение (7) представляет из себя матрицу , каждый столбец которой содержит коэффициенты передачи для элементов ВПС по одному из элементов ВВВ.
Петлевой коэффициент усиления в [3] приводится в виде:
 , , | (8) |
где Dз* = |E·eq - Aз| , Dp* = |E·eq - Ap| - Детерминанты замкнутой и разомкнутой систем. Также его можно выразить в виде отношения изображения решетчатой функций длительности импульса, которое определяетя в замкнутой системе (5) (обозначим ее - tвых[k]), к изображению решетчатой функции длительности импульса, подаваемого на вход разомкнутой системы (4) (обозначим ее - tвх[k]):
 , , | (9) |
Такое определение петлевого коэффициента вполне естественно, т.к. единственным управляющим воздействием для силовой части со стороны схемы управления в ИСН является длительность импульса. Подставляя q=j·ω·T (T-период коммутации) в (7)-(9) можно построить частотные характеристики дискретной системы в диапазоне частот 0 < ω < p/T, т.е. до половины частоты коммутации. В области более высоких частот эти характеристики не имеют физического смысла. Отметим, что характеристики расчитанные по формулам (8) и (9) ничем не отличаются друг от друга.
Применение метода усреднения для анализа ИСН состоит в том, что дискретная система заменяется некоторой непрерывной эквивалентной системой, поведение переменных в которой должно отражать поведение переменных реальной системы, усредненных за период коммутации [2]. Поведение переменных в разомкнутой системе, согласно усредненной модели (УМ), описывается нелинейным векторным дифференциальным уравнением:
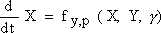 , , | (10) |
где X, Y, γ - ВПС, ВВВ и коэффициент заполнения, который для УМ выступает как некоторая непрерывная величина.
В замкнутой системе коэффициент заполнения в общем случае может быть представлен в виде функциональной зависимости:
| γ = fк(X,Y) | (11) |
Подстановка (11) в (10) позволяет получить нелинейное дифференциальное уравнение для замкнутой системы:
 , , | (12) |
где fу,з(X,Y)=fу,р (X,Y,fк(X,Y)).
Проводя линеаризацию (10)-(12) в точке установившегося режима, получим линейную модель:
 , , | (13) |
| δγ = bу·δX+vу·δY , | (14) |
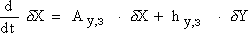 | (15) |
причем Aу,з=Aу, р+cу ·bу, hу,з=hу,р+cу ·vу
Коэффициент передачи для ВПС по внешним воздействиям получается после преобразования (15) по Лапласу:
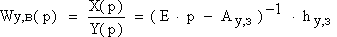 | (16) |
Петлевой коэффициент усиления можно получить аналогично (9) как отношение коэффициента заполнения γвых, определяемого выражением (14), к коэффициенту заполнения γвх, который входит в (13):
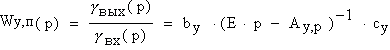 | (17) |
При подстановке p=j·ω в (16), (17) могут быть построены частотные характеристики линеаризованной непрерывной системы.
Первое из отличий характеристик РМ и УМ, указанных во введении, состоит в том, что характеристики РМ являются характеристиками дискретной системы, а характеристики УМ - непрерывной системы. Поэтому для адекватного сравнения этих характеристик необходимо приведение их к общему виду - дискретному или непрерывному.
Рассмотрим два векторно-матричных уравнения: разностное, описывающее некоторую линейную дискретную систему, и дифференциальное, описывающее некоторую непрерывную систему:
| X[k+1]=Aд · X[k] + hд · y[k], | (18) |
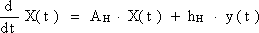 , , | (19) |
где X - ВПС, y - внешнее воздействие, которое для (18) - дискретное, а для (19) - непрерывное. При подаче ступенчатого воздействия на ту и другую системы ( y[k]=Y=const, при k>0; y(t)=Y=const, при t>0 ), решение (18) и (19) будет выглядеть, соответственно:
| X[k]=Aдk·X[0]+(Aдk-E)·(Aд-E)-1·hд·Y | (20) |
| X(t)=eAн·t·X(0)+(eAн·t-E)·Aн-1·hн·Y | (21) |
Сопоставляя полученные выражения, приходим к выводу, что при замене непрерывного аргумента в (21) на дискретный t=k·T, решение (21) будет идентично по форме решению (20), причем справедливы соотношения:
| Aд = eAн·T , | (22а) |
| (Aд-E)-1·hд = Aн-1·hн | (22б) |
Посредством такой замены непрерывного аргумента дискретным, мы фактически осуществляем выборки данных через временные интервалы равные периоду коммутации T, что позволяет перейти от рассмотрения непрерывной системы к рассмотрению некоторой эквивалентной дискретной системы, которая точно также реагирует на ступенчатое воздействие как и исходная система. При этом параметры этой системы будут выражаться через параметры исходной непрерывной системы следующим образом: Aд = eAн·T , hд=(Aд-E)·Aн-1·hн - см (22).
Наоборот, дискретной системе (18) можно сопоставить некоторую непрерывную систему (19). При этом параметры этой непрерывной системы выражаются через параметры исходной дискретной системы как: Aн = ln(Aд)/T , hн=Aн·(Aд-E)-1·hд (см 22).
Матрицу ln(Aд) можно определить, воспользовавшись каноническим представлением матрицы Aд [5]:
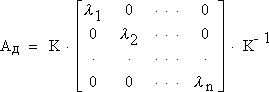 , ,
| (23) |
где K - преобразующая матрица. Диагональная матрица, расположенная между K и K-1 содержит собственные значения матрицы Aд и называется канонической формой матрицы Aд. Интересующая нас матрица выражается в этом случае как:

| (24) |
Таким образом дискретному коэффициенту передачи, полученному по (18):
 , ,
| (25) |
(где q=p·T) соответствует непрерывный коэффициент передачи:
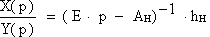 , ,
| (26) |
и наоборот. Такое преобразование в частотной области сходно с преобразованием приведенном в [6] для импульсных систем, и отличается от него тем, что оно получено при подаче ступенчатого, а не имульсного воздействия.
На рис.1 приведены ЛАЧХ и ФЧХ
петлевого коэффициента усиления расчитанного для РМ по формуле (9), для УМ по формуле (17) и для дискретного
представления усредненной модели (ДУМ) по формуле, полученной при преобразовании
(17) в дискретную форму способом
изложенным в предыдущем разделе. Эти характеристики были получены для
математических моделей (УМ и РМ) стабилизатора на основе идеального понижающего
преобразователя напряжения с ПД-коррекцией.
 - по РМ,
- по РМ,  - по УМ,
- по УМ,  - по ДУМ
- по ДУМ
Преобразователь имеет следующие параметры: значения индуктивности, емкости и сопротивления нагрузки - L=2.5 Гн, C=12.5 Ф, R=5 Ом. Напряжение источника питания Eп=10 В. Управление силовым ключем происходит так: в начале периода ключ замыкается; размыкание его происходит в момент, когда пилообразное напряжение Uп(t)=A-B·t/T (t - время прошедшее с начала периода), достигает значения некоторого напряжения Uш(t)=Uс(t)+Kт·iс(t) (назовем его напряжением на входе широтно-импульсного модулятора), где Uс - напряжение на емкости, iс - ток в ней, Kт - коэффициент связи, имеющий размерность сопротивления. Параметры управления следующие: T=1 с, A=5.128 В, B=0.246 В, Kт=0.111 Ом.
Как видно из рисунка характеристики УМ и РМ сильно отличаются вблизи половины частоты коммутации fк/2 (fк=1/T): ФЧХ полученная по УМ стремится к π/2, тогда как ФЧХ полученная по РМ равна нулю при fк/2. Последнее обстоятельство, как известно, обьясняет возникновение неустойчивости в дискретной системе, если значение ЛАЧХ на частоте fк/2 больше нуля. Общепринятым мнением является утверждение, что по УМ невозможно предсказать неустойчивость в такой системе, поскольку ФЧХ УМ никогда не достигает нулевого значения. Однако, как видно из рисунка, ФЧХ полученная по ДУМ пересекает ноль, и вообще, близка к характеристике ФЧХ полученной по РМ. Таким образом, оказывается возможным не только более адекватное сравнение характеристик, но и предсказание неустойчивости в замкнутой дискретной системе при использовании метода усреднения. Стоит отметить, что запас устойчивости, который дает ДУМ, оказывается несколько заниженным для ИСН с ПД-регулированием, поскольку наличие пульсаций в реальной системе делает ее более устойчивой.
Рассмотрим теперь вторую особенность сравнения характеристик, получаемых методами усреднения и разностных уравнений, касающуюся того, что поведение переменных УМ ближе к поведению средних значений переменных в реальной системе. Непрерывная функция описывающая поведение переменных состояния усредненных за период коммутации имеет вид:
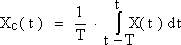
| (27) |
Поскольку задать аналитически такую функцию довольно трудно, воспользуемся зависимостью, которую можно получить, используя метод разностных уравнений:
| Xс[k] = fс(X[k-1],Y[k-1]), | (28) |
где fc - некоторая нелинейная векторная функция, позволяющая получить среднее за период значение ВПС, зная значение ВПС в начале периода и значение ВВВ для данного периода. Формула (28) определяет значение функции (27) в моменты k·T при воздействии на вход системы ВВВ, аппроксимированного ступенчатыми функциями.
Линеаризация (28) в точке установившегося режима дает для приращений:
| δXс[k]=ас·δX[k-1]+hс·δY[k-1] | (29) |
Отметим, что матрицы aс и hс могут быть определены аналитически через параметры системы и значения ВПС, ВВВ и длительности импульса в установившемся режиме.
Дискретное преобразование Лапласа выражения (29) позволяет получить дискретные коэффициенты передачи для средних значений ВПС по ВВВ:
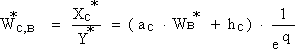
| (30) |
Эта формула позволяет получать дискретные частотные характеристики для средних значений переменных разностной модели (СРМ) при q=j·ω·T.
Для того, чтобы получить коэффициенты передачи для непрерывной области, выражение (29) нужно сначала привести к виду разностного уравнения (18). Решая совместно (29) и (6), получим в конечном итоге следующее рекуррентное соотношение для средних значений ВПС:
| δXс[k+1]=Aс·δXс[k]+hс·δY[k]+h1с·δY[k-1], | (31) |
где Aс=ac·Aз·aс-1 , h1c=ac·(hз - Aз·aс-1·hс).
Как видно из (31), при ступенчатом воздейсвии по ВВВ, на первом периоде (k=0) действует матрица hс, а на всех последующих - матрица h2с=hс+h1с. Поэтому (31) можно без большой погрешности аппроксимировать разностным уравнением:
| δXс[k+1]=Aс·δXс[k]+h2с·δY[k], | (32) |
Для данного аппроксимированного выражения для средних значений разностной модели можно получить непрерывную модель (НРМС), используя формулы (22) и (26), приведенные в предыдущем разделе.
На рис.2 показаны непрерывные
частотные характеристики, полученные по УМ, непрерывному представлению
разностной модели для мгновенных (НРМ) и средних (НРМС) значений коэффициента передачи "ток индуктивности/напряжение питания"(Il/Eп). Для наглядности, характеристики
построены до частоты, большей чем половина частоты коммутации. Как видно из
рисунка, имеется качественное отличие характеристик, получаемых по УМ и
характеристик НРМ. При этом характеристики УМ практически совпадают с
характеристиками, описывающими поведение средних значений переменных (НРМС).
Тоже самое можно сказать и о характеристиках, сравнение которых происходит в
дискретной области.
 - по УМ,
- по УМ,  - по НРМ,
- по НРМ,  - по НРМС
- по НРМС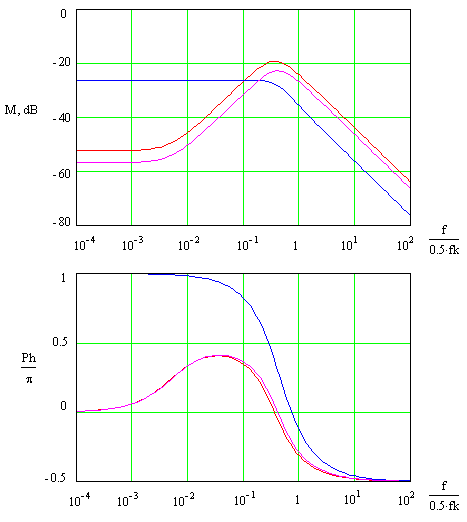
Приведенный пример показывает, что поведение мгновенных значений ВПС не всегда соответствует поведению их средних значений. Отметим, что отличия в характеристиках средних и мгновенных значений РМ в данной схеме не столь явно выражены для других коэффициентов передачи по ВВВ (Il/Jн, Uс/Eп, Uc/Jн, где Jн - ток нагрузки).
Отличие ЛАЧХ УМ от характеристик РМ (как для мгновенных так и средних величин) на нулевой частоте также обусловлено наличием пульсаций в дискретной системе. В ИСН с ПД-коррекцией коэффициенты передачи для выходного напряжения по напряжению питания и току нагрузки оказываются меньше по РМ, чем по УМ. Это обьясняется своеобразным параметрическим действием пульсаций на входе широтно-импульсного модулятора, которые в данной схеме в основном определяются формой тока в индуктивности. Так, например, при увеличении напряжения питания или снижении тока нагрузки (при наличии паразитного сопротивления дросселя), пульсации напряжения на индуктивности, а, следовательно, и на входе модулятора, возрастают, что приводит к уменьшению длительности импульса в системе.
1. Дана новая форма записи петлевого коэффициента усиления для разностой и усредненной моделей ИСН.
2. Показано, что качественное различие частотных характеристик на частоте близкой к половине частоты коммутации вызвано их неадекватным сравнением.
3. Показана принципиальная возможность предсказания неустойчивости в схеме при использовании метода усреднения.
4. Продемонстрировано, что поведение переменных в усредненной модели ближе к поведению средних значений переменных в дискретной системе, дан метод сравнения характеристик усредненной и разностной моделей с учетом этой особенности.
5. Изложен подход, позволяющий оценить, насколько усредненная модель адекватно отражает поведение переменных в дискретной системе в области малого сигнала, и на основании этого сделать выводы о применимости метода усреднения для анализа и проектирования того или иного класса схем.
[1] R.D.Middlebrook and S.Cuk, A general unified
approach to modelling switching converter power stages, IEEE PESC Record, p.p.
18-34, 1976.
[2] S.R.Sanders and G.C.Verghese, Synthesis of
averaged circuit models for switched power converters, IEEE Trans. Circuits
Syst. vol.38, No.8, p.p. 905-915, August 1991.
[3]
Мелешин В.И. Динамические свойства преобразователей с ШИМ-2 в режимах прерывистого и непрерывного токов. -
ЭТВА / Под ред. Ю.И.Конева. - М.: Радио и связь, 1986, вып. 17, с. 35-58.
[4]
Соболев Л.Б. О возможности применения
метода ЛЧХ к анализу преобразователей с переменной структурой. - ЭТВА / Под ред. Ю.И.Конева. - М.: Радио и
связь, 1986, вып. 17, с. 88-95.
[5]
Бромберг П.В. Матричные методы в теории релейного и импульсного регулирования,
М.: Наука, 1967.
[6]
Цыпкин Я.З. Теория линейных импульсных систем, М.: Физматгиз, 1963.
© 1998, © 2008 Бердников Д.В.