где
Дискретное преобразование Лапласа приведенных соотношений позволяет получить петлевой коэффициент усиления:
(где 1- единичная матрица) и коэффициенты передачи для ВПС по ВВВ:
Последний коэффициент представляет из себя матрицу, каждый столбец которой содержит коэффициенты передачи для элементов ВПС по одному из элементов ВВВ.
В о в т о р о й г л а в е предложены способы сравнения характеристик получаемых по УМ и РМ ИСН. Поскольку УМ представляет из себя непрерывную, а РМ - дискретную системы, адекватное сравнение их характеристик (в первую очередь - частотных) возможно только при учете этого различия. С другой стороны принцип построения УМ состоит в том, что дифференциальные уравнения описывающие поведение переменных состояния на различных интервалах детерминированной структуры схемы интегрируются (усредняются) за период коммутации. Поэтому поведение переменных УМ отражает поведение не мгновенных, а усредненных за период коммутации значений переменных состояния исходной системы. Следовательно, сравнение характеристик УМ целесообразно проводить не с характеристиками, отражающими поведение мгновенных значений переменных в начале периода, которые приводились в Главе 1, а с характеристиками, отражающими поведение средних значений переменных.
Используя метод усреднения для ИСН, можно получить линейную модель, описывающуюся следующими векторно-матричными дифференциальными уравнениями:
для разомкнутой системы
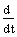 δX = Aу,р·δX +
hу,р·δY +
cу,р·δγ ,
δX = Aу,р·δX +
hу,р·δY +
cу,р·δγ ,
где γ - коэффициент заполнения,
для
коэффициента заполнения в замкнутой системе
для замкнутой системы
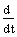 δX = Aу,з·δX +
hу,з·δY ,
δX = Aу,з·δX +
hу,з·δY ,
причем
Применив преобразование Лапласа к данным уравнениям, получим петлевой коэффициент усиления и коэффициенты для ВПС по ВВВ:
Подстановка
Для более адекватного сравнения этих частотных характеристик предлагается их преобразование в общую форму: непрерывную или дискретную. Пусть дискретная и непрерывная системы описываются, соответственно, матричными разностным и дифференциальным уравнениями:
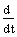 X(t) = Aн ·X(t) +
hн · y(t) ,
X(t) = Aн ·X(t) +
hн · y(t) ,
Тогда
при подаче ступенчатого воздействия на вход дискретной
Сопоставляя
полученные выражения, приходим к выводу, что при замене непрерывного аргумента
на дискретный (t = kT) оба решения идентичны по форме, причем справедливы
соотношения:
Используя указанное преобразование, сравнивались частотные характеристики РМ и УМ. На рис.1 показаны характеристики петлевого коэффициента усиления ИСН построенного на основе понижающего преобразователя напряжения с ПД-коррекцией, полученные по РМ, по УМ и по УМ преобразованной в дискретную форму (ДУМ). Как видно из рисунка, ФЧХ УМ качественно отличается от ФЧХ РМ на частотах близких к половине частоты коммутации (π/T), в то время как ФЧХ ДУМ практически совпадает с РМ. Отметим, что то обстоятельство, что ФЧХ ДУМ достигает нулевого значения на частоте половины частоты коммутации позволяет предсказать неустойчивость ИСН, когда ЛАЧХ на этой частоте больше нуля. Используя обычные характеристики УМ этого сделать нельзя.
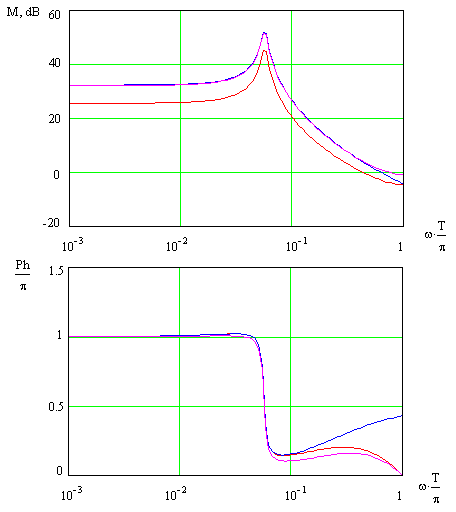
Рис.1 ЛАЧХ и ФЧХ петлевого кожффициента усиления:
 - по разностной модели (РМ), - по разностной модели (РМ),  - по усредненной модели (УМ), - по усредненной модели (УМ),  - по по дискретному представлению усредненной модели (ДУМ). - по по дискретному представлению усредненной модели (ДУМ). |
Кроме того, было проведено сравнение характеристик коэффициентов передачи для переменных по внешним воздействиям для УМ с характеристиками значений переменных состояния РМ усредненных за период коммутации. При этом для средних значений переменных были получены характеристики как в дискретной, так и в непрерывной форме. Для ИСН на основе преобразователя понижающего типа с ШИМ-2 и ПД-корекций ЛАЧХ характеристик УМ и средних значений переменных РМ отличаются на некоторую постоянную величину. Это отличие обусловлено своеобразным параметрическим действием пульсаций на входе широтно-импульсного модулятора, форма которых в основном определяется формой тока в дросселе. Уточнение УМ ИСН возможно путем учета пульсаций на входе модулятора. При этом коэффициент заполнения выражается через среднее значение ВПС, которое соответствует моменту коммутации, когда пилообразное напряжение широтно-импульсного модулятора оказывается равным не среднему значению напряжения на входе модулятора (как в обычной УМ), а его мгновенному значению в реальной схеме. Для такого варианта УМ коэффициенты передачи для ВПС по ВВВ оказываются очень близки к характеристикам полученным для средних значений ВПС по РМ, а петлевой коэффициент совпадает с полученным по обычной УМ. Это говорит о том, что учет пульсаций на входе модулятора позволяет смоделировать дополнительные параметрические связи по элементам ВВВ, влияющие на формирование коэффициента заполнения.
В т р е т ь е й г л а в е описываются методы, позволяющие извлекать некоторую дополнительную информацию из результатов расчета переходных процессов в ИСН, в частности, при имитационном моделировании с применением программы анализа электронных схем типа PSpice.
Для ускоренного определения установившегося режима в так называемых многопериодных схемах ( то есть в таких схемах, где длительность переходных процессов может занимать сотни или даже тысячи периодов коммутации) применяется метод экстраполяции. В третьей главе этот метод модифицирован применительно к стандартной системе анализа переходных процессов PSpice, какие-либо изменения в которой невозможны. Кроме того здесь указывается на возможность повышения точности за счет увеличения кратности выборки данных и косвенной проверки правильности получаемых результатов при расчете с различным сдвигом в данных. Там же дан простой критерий достижения установившегося режима заключающийся в сравнении разности значений каждой переменной в конце и начале периода с максимальной разницей мгновенных значений переменных внутри периода.
При имитационном моделировании ИСН с использованием PSpice возможность непосредственно получить частотные характеристики системы, линеаризованной в точке покоя, отсутствует. Но можно получить переходные или импульсные характеристики дискретной системы. Данные, полученные в результате расчета процессов во временной области могут быть пересчитаны в частотные характеристики с помощью дискретного преобразования Фурье. При подаче на вход дискретной системы ступенчатого или импульсного воздействия амплитудой Δx выражение частотного коэффициента передачи для выходной переменной у, запишется следующим образом. Для ступенчатого воздействия:
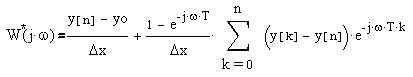
Для импульсного воздействия:
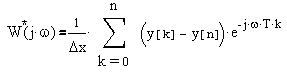 ,
,
где y[k] - решетчатая функция значений выходной величины (k = 0...n), уо - значение этой величины до подачи возмущающего воздействия.
В третьей главе также изложен метод, позволяющий определить коэффициенты разностного уравнения, описывающего ИСН на малом сигнале (приведенного в Главе 1) по результатам расчета переходных процессов. Пользуясь этим методом, можно определить все матрицы малосигнальной разностной модели. Для их определения должны быть получены переходные характеристики ИСН для каждой из переменных состояния по каждому элементу ВВВ и по тестовому воздействию по времени импульса в замкнутой системе. Число рассчитанных периодов может быть не больше 1+m, где m - порядок системы. Таким образом можно получить аналитическую дискретную малосигнальную модель для системы, аналитическое описание которой в общем случае неизвестно. С помощью этой модели можно исследовать различные переходные процессы для приращений переменных на малом сигнале и получить частотные характеристики.
В ч е т в е р т о й г л а в е рассматривается синтез ИСН (выбор закона регулирования и расчет его параметров) с использованием УМ и РМ. Основные два подхода к коррекции динамических характеристик - это последовательная и параллельная коррекции. В первом случае коррекция динамических свойств схемы по УМ осуществляется путем включения некоторого динамического звена коррекции сразу за динамическим звеном силовой части, а во втором - за счет введения в закон регулирования параллельной связи по некоторой дополнительной переменной (часто - по току дросселя).
Все
виды широтно-импульсной модуляции могут быть сведены по УМ к уравнению
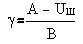 , где γ - коэффициент заполнения, Uш - напряжение на входе широтноимпульсного
модулятора, А, В - параметры модулятора, которые могут трактоваться как
напряжение опоры и амплитуда пилообразного напряжения, соответственно. Для
случая последовательной коррекции напряжения на входе широтно-импульсного модулятора
выражается как
, где γ - коэффициент заполнения, Uш - напряжение на входе широтноимпульсного
модулятора, А, В - параметры модулятора, которые могут трактоваться как
напряжение опоры и амплитуда пилообразного напряжения, соответственно. Для
случая последовательной коррекции напряжения на входе широтно-импульсного модулятора
выражается как
В
случае ПД-коррекции корректирующее звено Wк представляет из себя
дифференцирующее звено
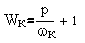 (одно или несколько
включенных последовательно, в зависимости от силовой части). Выбор необходимой
частоты (частот) звена коррекции осуществлялся исходя из значения коэффициента
(коэффициентов) затухания колебательного звена (звеньев) стоящих в знаменателе
коэффициентов передачи замкнутой системы.
При синтезе Wк минимально-возможным значением коэффициента затухания
было задано число 0.7. При этом обеспечивается достаточно высокое
быстродействие замкнутой системы при отсутствии заметных колебаний на
резонансных частотах для выходной величины (напряжения нагрузки).
(одно или несколько
включенных последовательно, в зависимости от силовой части). Выбор необходимой
частоты (частот) звена коррекции осуществлялся исходя из значения коэффициента
(коэффициентов) затухания колебательного звена (звеньев) стоящих в знаменателе
коэффициентов передачи замкнутой системы.
При синтезе Wк минимально-возможным значением коэффициента затухания
было задано число 0.7. При этом обеспечивается достаточно высокое
быстродействие замкнутой системы при отсутствии заметных колебаний на
резонансных частотах для выходной величины (напряжения нагрузки).
Для случая коррекции последовательного типа было также рассмотрено применение ПИД коррекции, отличающееся от ПД коррекции увеличением петлевого коэффициента усиления на низких частотах за счет введения дополнительного ПИ-звена. Также было описано введение дополнительных параметрических связей в закон регулирования, позволяющее снизить влияние изменения внешних воздействий (напряжения питания и тока нагрузки) на напряжение нагрузки ИСН как в статике, так и в динамике.
Реализация последовательной коррекции в реальном ИСН зависит от того как соотносится поведение мгновенных значений тех или иных величин с поведением их средних значений. Так ПД-коррекция для ИСН с ШИМ-2 на основе понижающего преобразователя может быть осуществлена путем включения последовательно с ИСН реального дифференцирующего звена или введения связи по мгновенному значению тока выходного конденсатора, а для ИСН на основе повышающего преобразователя этого сделать невозможно. Это происходит потому, что в последнем случае поведение тока конденсатора в течение первого интервала детерминированной структуры схемы отличается от поведения среднего значения тока конденсатора ( в частности, мгновенный ток конденсатора не зависит от тока дросселя, тогда как средний ток зависит от него). Для адекватной реализации ПД-коррекции для повышающего преобразователя предложено введение дополнительных связей в закон регулирования по току дросселя, подвергающегося интегрированию за время включенного состояния ключа. Способы осуществления ПД - коррекции для ИСН на основе понижающего и повышающего преобразователей проверены также экспериментально. Результаты исследования макетов приведены в Приложении 2.
В рассмотренном случае синтеза по УМ ИСН с параллельной коррекцией напряжение на входе модулятора Uш уже нельзя принимать равным Uн на нулевой частоте, поскольку Uш зависит также от тока дросселя, а следовательно, и от тока нагрузки. Для обеспечения требуемых статических характеристик необходимо увеличить коэффициент усиления на нулевой частоте за счет введения дополнительного ПИ-звена в ветвь связи по напряжению на нагрузке.
При
синтезе ИСН с параллельной коррекцией по РМ ставилась задача удержания
выходного напряжения ИСН в некотором “коридоре” при любых изменениях параметров
схемы в заданном диапазоне значений. При этом сохранялось требования высокого
быстродействия и отсутствия колебаний на
резонансных частотах. Эта задача решалась для ИСН построенных на основе
преобразователей напряжения с силовой частью второго порядка. Для ее решения
необходимо было выбрать коэффициенты c0...c2 уравнения замыкания
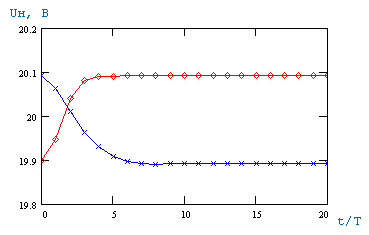
 -
прямой переход
-
прямой переход
 - обратный переход
- обратный переходРис.2 Характеристики предельных переходов в ИСН на основе повышающего преобразователя напряжения с параллельной коррекцией.
ЗАКЛЮЧЕНИЕ.
1. Рассмотрен анализ динамических характеристик ИСН с использованием метода разностных уравнений. При этом наряду с мгновенными, исследовались усредненные за период коммутации значения переменных, что позволило получить более полную информацию о динамических свойствах ИСН. Построение разностной модели ИСН проведено в матричном виде и ориентировано на применение для ее реализации математической системы MathCAD, что позволило при сохранении высокой точности расчетов, максимально приблизить эту модель к инженерной практике.
2. Предложен подход к сравнению характеристик (в первую очередь - частотных), полученных с помощью усредненной и разностной моделей, учитывающий их различие, в частности - дискретный характер разностной, и непрерывный - усредненной модели. Наряду с более адекватным сравнением характеристик, этот подход принципиально позволяет предсказать неустойчивость реального ИСН при анализе по усредненной модели.
3. Рассмотрены методы получения некоторых дополнительных характеристик по результатам анализа переходных процессов с помощью программы имитационного моделирования типа PSpice. В частности: метод ускоренного нахождения установившегося режима, метод расчета частотных характеристик дискретной системы и метод, позволяющий вычислять коэффициенты линеаризованного разностного уравнения, описывающего ИСН на малом сигнале. Применение этих методов позволяет расширить возможности иммитационного моделирования.
4. Рассмотрены методики синтеза ИСН (выбора параметров закона управления ) по усредненной модели с использованием коррекции последовательного и параллельного типов, а также синтеза по разностной модели с использованием параллельной коррекции. Эти методики позволяют добиться хороших динамических характеристик на малом (в первом случае) и на большом (во втором случае) сигналах.
Основные результаты диссертации отражены в работах:
1. Бердников Д.В., Недолужко И.Г. Расчет установившегося режима многопериодных схем. // Радиотехника. - 1996 - №1 - с. 44-45.
2. Бердников Д. В., Недолужко И. Г. Сравнение непрерывной и дискретной моделей импульсных преобразователей напряжения. - М., 1998. - 9 с., - Деп. в ВИНИТИ 02.03.1998, № 604-В1998.
3. Бердников Д. В. О сравнении частотных характеристик усредненной и разностной моделей ИСН с ШИМ. - М., 1998. - 18 с. - Деп. в ВИНИТИ 02.03.1998, № 606-В1998
4. Бердников Д. В. Применение метода разностных уравнений для синтеза ИСН. - М., 1998. - 13 с. - Деп. в ВИНИТИ 02.03.1998, № 605-В1998
© 1998, © 2008 Бердников Д.В.